Air That is Pushed Upward and Continues to Move Upward is Defined as
Chapter 5: Atmospheric Stability
Alison Nugent and David DeCou
Learning Objectives
By the end of this chapter, you should be able to:
- Interpret stability based on the dry and moist adiabatic lapse rates
- Understand how stability relates to vertical motion in the atmosphere
- Describe and differentiate between the many lines on a Skew-T log-P diagram
- Find the LCL, regions of CAPE and CIN, and the tropopause from a Skew-T log-P diagram

When you think of the word "stable," you typically think of an object that is unlikely to change or something that is balanced. The opposite is true with something that is "unstable". An unstable object is likely to fall or change position with time. The same is true with clouds. When you see a fluffy cumulus cloud, you might notice them changing shape from one minute to the next. Such clouds are in a constant state of change, and thus represent the atmosphere in an unstable state.

Instability in the atmosphere is a concept that is intimately connected with thunderstorms, cumulus development, and vertical motion. In order to visualize the concept of stability, you might imagine a boulder sitting at the bottom of a canyon surrounded by steep hills, as depicted in the figure below by the blue circle. If you were strong enough to push the boulder from its initial position partway up one of the hills, it would roll back to the bottom once you let go. Despite exerting a force on the boulder and causing an initial displacement, it would return to its initial position, and the net displacement would be zero. To visualize the concept of instability, imagine the same boulder at the top of a hill (red circle below). If you were able to push the boulder just a little bit in any direction, it would begin to roll downward and accelerate away from its initial position. However, if the same boulder were to be placed on flat ground (green circle below) and you were to push it, it would change position, but remain in its new position. This is an example of neutral stability.
Each of these concepts can be applied to motions of air parcels in the atmosphere. The topic of stability in atmospheric science is important because the formation of clouds is closely related to stability or instability in the atmosphere. In this chapter we will connect these concepts to the buoyancy of air parcels, and learn to use thermodynamic diagrams to visualize movement.

Adiabatic Processes
When discussing stability in atmospheric sciences, we typically think about air parcels, or imaginary blobs of air that can expand and contract freely, but do not mix with the air around them or break apart. The key piece of information is that movement of air parcels in the atmosphere can be estimated as an adiabatic process. Adiabatic processes do not exchange heat and they are reversible.
Imagine you have a parcel of air at the Earth's surface. The air parcel has the same temperature and pressure as the surrounding air, which we will call the environment. If you were to lift the air parcel, it would find itself in a place where the surrounding environmental air pressure is lower, because we know that pressure decreases with height. Because the environmental air pressure outside the parcel is lower than the pressure inside the parcel, the air molecules inside the parcel will effectively push outward on the walls of the parcel and expand adiabatically. The air molecules inside the parcel must use some of their own energy in order to expand the air parcel's walls, so the temperature inside the parcel decreases as the internal energy decreases. To summarize, rising air parcels expand and cool adiabatically without exchanging heat with the environment.
Now imagine that you move the same air parcel back to Earth's surface. The air parcel is moving into an environment with higher air pressure. The higher environmental pressure will push inward on the parcel walls, causing them to compress, and raise the inside temperature.
The process is adiabatic, so again, no heat is exchanged with the environment. However, temperature changes in the air parcel can still occur, but it is not due to mixing, it is due to changes in the internal energy of the air parcel.
Dry Adiabatic Lapse Rate
As long as an air parcel is unsaturated (relative humidity < 100%), the rate at which its temperature will change will be constant. A decrease in temperature with height is called alapse rate and while the temperature decreases with altitude, it is defined as positive because it is a lapse rate. Recall from chapter 3 that the dry adiabatic lapse rate, Γd , is equal to 9.8 K·km-1 = 9.8 °C·km-1 . This drop in temperature is due to adiabatic expansion and a decrease in internal energy.

Let's get back to the topic of atmospheric stability. Stability in the atmosphere refers to a condition of equilibrium. As discussed with the example of the boulder on a hill or valley, some initial movement resulted in either more (unstable), less (stable), or no change (neutral). Given some initial change in the elevation of an air parcel, if the air is in stable equilibrium, the parcel will tend to return back to its original position after it is forced to rise or sink. In an unstable equilibrium, an air parcel will accelerate away from its initial position after being pushed. The motion could be upward or downward, but generally unstable atmospheres favors vertical motions. Finally, in a neutral equilibrium, some initial change in the elevation of an air parcel will not result in any additional movement.
Determining Stability
How do you know if an air parcel will be stable after some initial displacement? Stability is determined by comparing the temperature of a rising or sinking air parcel to the environmental air temperature. Imagine the following: at some initial time, an air parcel has the same temperature and pressure as its environment. If you lift the air parcel some distance, its temperature drops by 9.8 K·km-1, which is the dry adiabatic lapse rate. If the air parcel is colder than the environment in its new position, it will have higher density and tend to sink back to its original position. In this case, the air is stable because vertical motion is resisted. If the rising air is warmer and less dense than the surrounding air, it will continue to rise until it reaches some new equilibrium where its temperature matches the environmental temperature. In this case, because an initial change is amplified, the air parcel is unstable. In order to figure out if the air parcel is unstable or not we must know the temperature of both the rising air and the environment at different altitudes.
One way this is done in practice is with a weather balloon. We can get a vertical profile of the environmental lapse rate by releasing a radiosonde attached to a weather balloon. A radiosonde sends back data on temperature, humidity, wind, and position, which are plotted on a thermodynamic diagram. This vertical plot of temperature and other variables is known as a sounding.
Dry Stability
If an air parcel is dry, meaning unsaturated, stability is relatively straightforward. An atmosphere where the environmental lapse rate is the same as the dry adiabatic lapse rate, meaning that the temperature in the environment also drops by 9.8 K·km-1, will be considered neutrally stable. After some initial vertical displacement, the temperature of the air parcel will always be the same as the environment so no further change in position is expected.
If the environmental lapse rate is less than the dry adiabatic lapse rate, some initial vertical displacement of the air parcel will result in the air parcel either being colder than the environment (if lifted), or warmer than the environment (if pushed downward). This is because if lifted, the temperature of the air parcel would drop more than the temperature of the environment. This is a stable situation for a dry air parcel and a typical scenario in the atmosphere. The global average tropospheric lapse rate is 6.5 K·km-1 , which is stable for dry lifting.
Finally, if the environmental lapse rate is greater than the dry adiabatic lapse rate, some initial vertical displacement of the air parcel will result in the air parcel either being warmer than the environment (if lifted), or colder than the environment (if pushed downward). This is because if lifted, the temperature of the air parcel would drop less than the temperature of the environment. This is an unstable situation for a dry air parcel.
In general for a dry air parcel, the following is true.
Moist Adiabatic Lapse Rate
When moisture is added, everything gets more complicated. In Chapter 4 we learned that whether or not an air parcel is saturated depends primarily on its temperature and, of course, its moisture content. The graph of the Clausius-Clapeyron relationship shows us that given the same amount of moisture, air is more likely to be saturated at a lower temperature.
We know that as an air parcel is lifted, its temperature drops according to the dry adiabatic lapse rate. So what happens when the air parcel is cold enough that the air becomes saturated with respect to water vapor? The short answer is that if it continues to cool, water vapor will condense to liquid water to form a cloud.
When water vapor condenses, it goes from a higher energy state to a lower energy state. Energy is never created nor destroyed, especially in phase changes, so what happens to all that excess energy? The energy gets released in the form of latent heat. The latent heat of condensation is approximately equal to 2.5 * 106 J·kg-1, which means that for every kg of water vapor that condenses to form liquid water, 2.5 *106 Joules of energy are released.
This has large consequences for the lapse rate of an air parcel and distinguishes the dry adiabatic lapse rate from the moist adiabatic lapse rate. As latent heat is added from the process of condensation, it offsets some of the adiabatic cooling from expansion. Because of this, the air parcel will no longer cool at the dry adiabatic lapse rate, but will cool as a slower rate, known as the moist adiabatic lapse rate. To summarize, a parcel will cool at the dry adiabatic rate until it is saturated, after which it won't cool as quickly due to condensation. The moist adiabatic lapse rate varies a little by temperature, but in this class we will consider it a constant for simplicity:Γm = 4.5 K·km-1 = 4.5 °C·km-1
Moist Stability
The effects of moisture change the lapse rate of the air parcel and, therefore, affects stability. However, the concepts are still the same and we still compare the air parcel temperature to the environmental temperature. We have just one added complication to worry about—we need to know whether the air parcel is dry or moist. Some definitions are included below, which take into account both dry and moist adiabatic lapse rates.
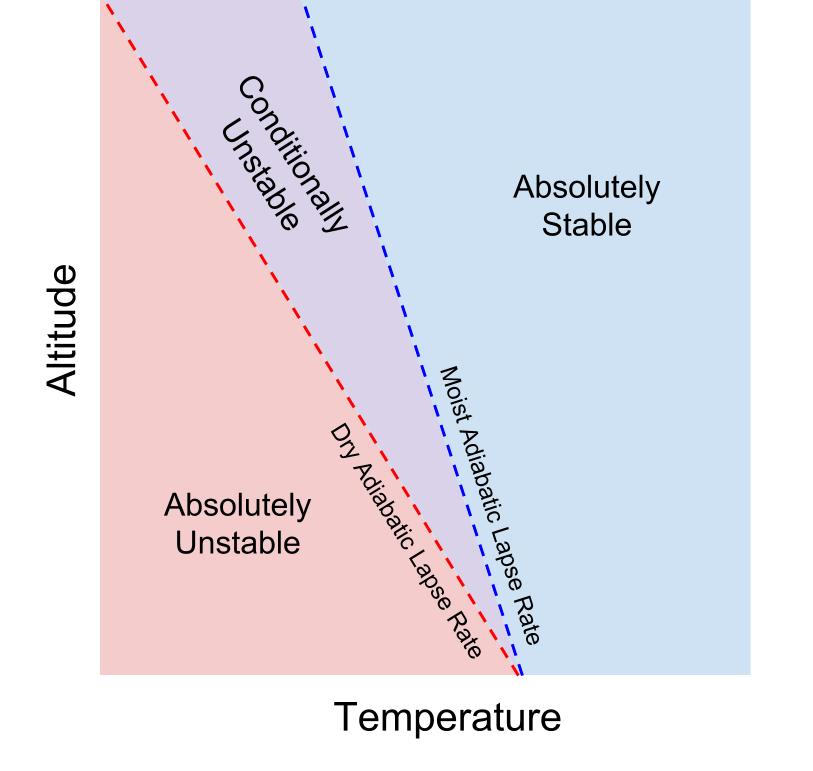
The atmosphere is said to be absolutely stable if the environmental lapse rate is less than the moist adiabatic lapse rate. This means that a rising air parcel will always cool at a faster rate than the environment, even after it reaches saturation. If an air parcel is cooler at all levels, then it will not be able to rise, even after it becomes saturated (when latent heating will counteract some cooling).
The atmosphere is said to be absolutely unstable if the environmental lapse rate is greater than the dry adiabatic lapse rate. This means that a rising air parcel will always cool at a slower rate than the environment, even when it is unsaturated. This means that it will be warmer (and less dense) than the environment, and allowed to rise.
The atmosphere is said to be conditionally unstable if the environmental lapse rate is between the moist and dry adiabatic lapse rates. This means that the buoyancy (the ability of an air parcel to rise) of an air parcel depends on whether or not it is saturated. In a conditionally unstable atmosphere, an air parcel will resist vertical motion when it is unsaturated, because it will cool faster than the environment at the dry adiabatic lapse rate. If it is forced to rise and is able to become saturated, however, it will cool at the moist adiabatic lapse rate. In this case, it will cool slower than the environment, become warmer than the environment, and will rise.
Hawaiian Focus Box
Around Hawaii, the atmosphere is almost always conditionally unstable, meaning that the environmental lapse rate lies somewhere between the dry and moist adiabatic lapse rates. For this reason, Hawaii almost always has convective clouds. Convective clouds are clouds where the edges are bumpy and cumuliform, like cauliflower. The clouds are convective because the atmosphere is stable to dry lifting and unstable to moist lifting. Once the air is saturated, instability sets in and vertical motion takes off. This is especially common as air is lifted over our mountainous islands. The forced lifting from the terrain creates clouds and rain right over the mountains! In scientific terms, the initial lifting of the stable low level dry air by the terrain causes the air to adiabatically expand and reach saturation, at which point the environment is unstable to moist lifting and convection is the result.
There are many different types of thermodynamic diagrams, but the main one we will discuss are Skew-T Log-P diagrams, so-named because the isotherms (lines of equal temperature, T) on the diagram are slanted (skewed) and the isobars (lines of equal pressure, P) on the diagram are in log space. Here we will focus on how to read and utilize Skew-T Log-P diagrams (often shortened to Skew-T diagram) to determine parcel buoyancy and atmospheric stability.
The radiosonde balloon sounding plotted here was launched from Lihue on Kauai (see the top left, labelled as station "91165 PHLI Lihue"). You can see the vertical environmental temperature profile (T) plotted as the black jagged line on the right. The dew point temperature (Td) with height is plotted with the black jagged line on the left. Although this figure may be overwhelming to read at first, we'll walk through it together. The horizontal axis is temperature in °C, with temperatures increasing to the right. The vertical axis is air pressure in hPa, decreasing with height, so higher heights are toward the top of the chart. When the T and Td lines are close together, the environment has a high relative humidity and the air is closer to saturation. In this particular sounding, there is a lot of moisture near the surface, but dries out in the mid-levels.
Radiosonde balloons are launched twice a day (00Z and 12Z) from many locations around the world. The latitude and longitude for the station is given in the top of the list on the right where station latitude (SLAT) is given as 21.99 degrees North and SLON is -159.34 degrees West. The station elevation SELV is 30 m. The sounding time and date is given in the bottom left, and the bottom right says "University of Wyoming" because in this particular example, the University of Wyoming is the organization that gathered and archived the dataset. You can find soundings for other locations and dates at this website: http://weather.uwyo.edu/upperair/sounding.html.
Let's go through the lines one by one.

The horizontal lines on a Skew-T are isobars, or lines of equal air pressure. You will typically see them given in hPa, but the lines in the above figure are in kPa. The isobars have larger spaces as you get toward the top of the diagram because they are logarithmic with height. The evenly-spaced solid lines that slant up and to the right are isotherms, or lines of equal temperature (T). This allows colder temperatures to be plotted on the diagram.

The dashed lines that run up and to the right are isohumes, or lines of constant mixing ratio. These are typically given in units of g·kg–1. If you use a Skew-T where these lines are not dashed or color-coded, remember that these are spaced more closely together than isotherms and are more steep. They also do not line up with the temperature labels on the x-axis.

The evenly-spaced curved solid lines that run from bottom right to top left are dry adiabats, and depict the dry adiabatic lapse rate (9.8 K·km-1). The dry adiabatic lapse rate is considered a constant, but you can see here that over large changes in temperature and pressure, it varies a little. Don't worry about these variations—we still consider it a constant. Dry adiabatic lapse rate reference lines are also called lines of constant potential temperature (θ). The dry adiabats always curve upward from right to left in a concave way.

The uneven, dashed, lines that curve up and to the left are the moist adiabats. The moist adiabatic lapse rate varies with both temperature and moisture content, but is close to the dry adiabatic lapse rate at high altitudes due to cold temperatures and small moisture content. These lines are parallel to the dry adiabats higher up on the Skew-T Log-P diagram. These are also lines of constant equivalent potential temperature (θe).
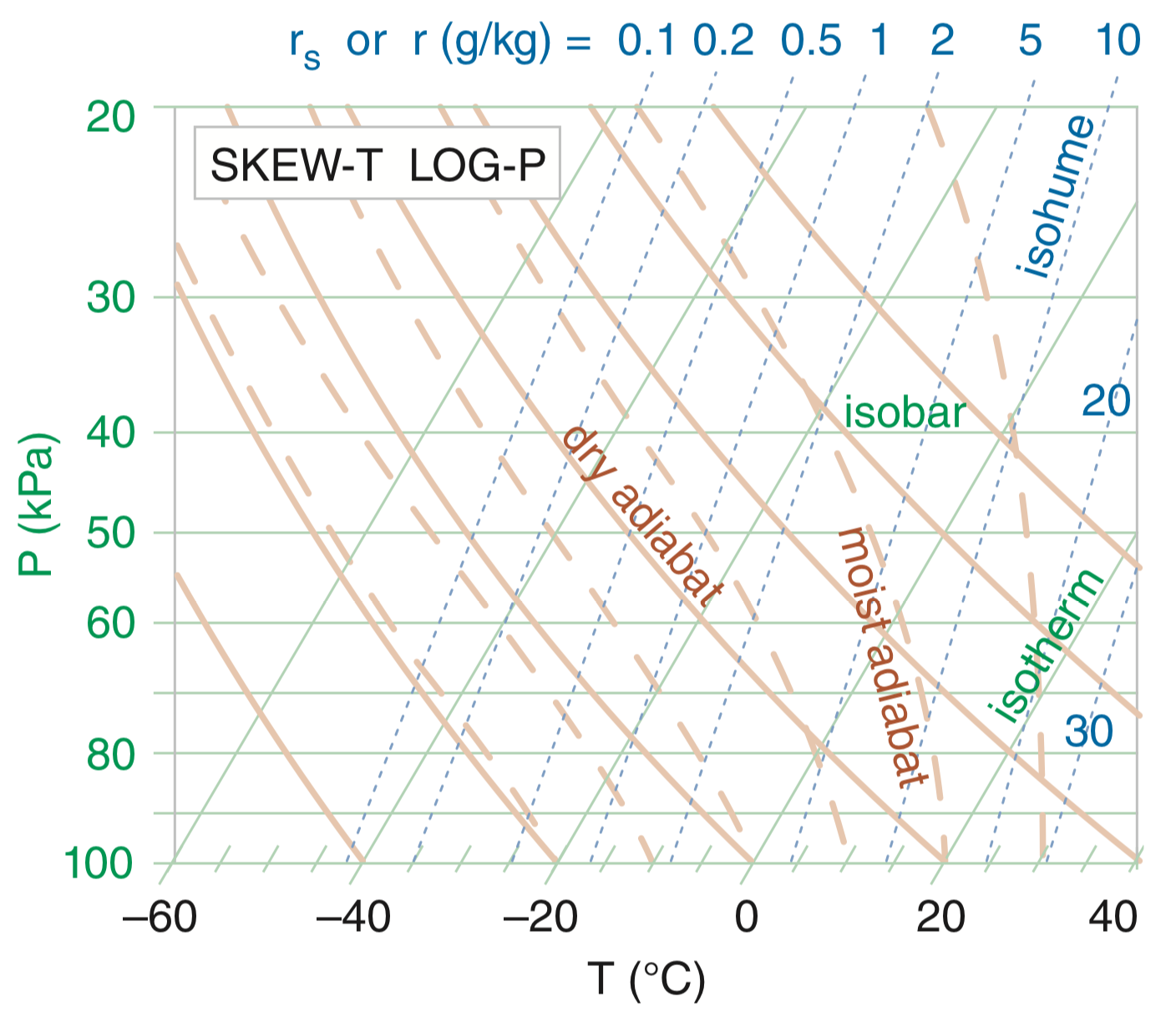
Here is a complete Skew-T Log-P diagram. All of the lines look confusing and complicated when combined, but each represents a constant change in one variable.
Let's look at another real balloon sounding. This time launched from Hilo during Hurricane Lane.
On this Skew-T diagram, all of the same lines are there. Horizontal blue lines are isobars, slanted blue lines are isotherms, slanted purple lines are isohumes, the green lines are the dry adiabats, and the blue curved lines are the moist adiabats. The T (right) and Td (left) black lines are close together and sometimes overlap in the lowest 500 hPa of the atmosphere because the lower levels are incredibly moist, and a deep cloud layer extended up to nearly 6 km altitude.
Finding the Lifting Condensation Level (LCL)
When plotting a sounding on a Skew-T diagram, you may have a selection of data similar to the example given below. You will likely have pressure, temperature (T), and a dew point temperature (Td) with altitude.

In order to plot the sounding, it is easiest to start by finding the pressure level and then move to the right to plot the temperature and dew point temperature. Pay careful attention to the fact that the isotherms are skewed. Rotate the axis in your mind when you plot your temperature and dew point. Once you have plotted all of your temperatures and dew points, you will have a vertical temperature and humidity profile of the atmosphere.

Now that we plotted the sounding, it is useful to know how a rising air parcel will behave when placed in this environment. Is the atmosphere stable, unstable, or conditionally unstable? We can determine this by estimating the rate at which a rising parcel will cool and drawing a parcel path upward. A rising air parcel will cool at the dry adiabatic lapse rate until it is saturated, after which it will cool at the moist adiabatic lapse rate. How do we know when a parcel will be saturated? First we need to find the Lifting Condensation Level (LCL).
The Lifting Condensation Level (LCL) is the level at which the water vapor in an air parcel that is lifted dry adiabatically will be saturated.

To find the LCL, start at the surface (or the pressure level closest to the surface, typically 1000 hPa) and plot the temperature and dewpoint temperature. In the case of the example above, the surface pressure level must be at a raised elevation with Psurf= 90 kPa or 900 hPa, T = 30 °C, and Td= -10 °C. Imagine that the air parcel has the same temperature and dewpoint temperature as the environment at first. Initially, it will cool at the dry adiabatic lapse rate as it rises. First, follow the surface temperature upward along a dry adiabat. In all likelihood, the temperature will not be directly along a marked dry adiabat line as it is in the example so follow a line upward parallel to a dry adiabat. Similarly, start at your surface dew point and follow the isohume (constant mixing ratio line) upward because the moisture content of the air parcel does not change with dry lifting. Draw these lines upward until they intersect. This intersection will give you the level of the lifting condensation level (LCL).


In this example, the surface temperature and dewpoint temperature line up nicely with an isohume and a dry adiabat line, but this typically won't be the case with a real sounding. The procedure, however, will be the same. The LCL marks the approximate cloud base height for convective clouds (cumulus type), where rising air first becomes saturated.
After the air parcel has been lifted dry adiabatically to the LCL, it becomes saturated. As we know, a saturated air parcel cools at the smallermoist adiabatic lapse rate. From the LCL, follow a line parallel to a moist adiabat upward to get the approximate lapse rate of your parcel as it rises. In the example soundings from Hilo and Lihue shown earlier, this same line is plotted in a light grey color from the surface all the way up in the atmosphere. It shows the temperature a surface based parcel would have when lifted through the troposphere.
As you follow an air parcel temperature upward moist adiabatically, the point at which it intersects the environmental temperature profile (where your parcel becomes warmer than its environment) is called the Level of Free Convection, or the LFC.
As you continue following the air parcel path upward moist adiabatically from the LFC, the point where it intersects the sounding again (the point where your parcel becomes cooler than its environment) is called the Equilibrium Level (EL).
Normand's Rule for Wet-bulb Temperature
You can estimate the surface wet bulb temperature by taking the LCL example one step further. Normand's Rule is used to calculate the wet-bulb temperature from the air temperature and the dew point temperature. The wet bulb temperature is always between the dew point and the dry bulb temperature (Td ≤ Tw ≤ T). To find the wet bulb temperature on a Skew-T Log-Pdiagram, follow the surface T upwards along a dry adiabat, and the surface Td upwards along a isohume. Where they meet is the LCL, as just explained. Next, follow a moist adiabat back down to the surface. Where the moist adiabat intersects the surface is the wet-bulb temperature value.
CAPE & CIN
The "positive area" between the parcel path and the environmental temperature profile, traced out between the LFC and the EL (where the parcel is warmer than the environment) gives a measure of the Convective Available Potential Energy, or CAPE, given in units of J·kg–1. This is an estimate of the buoyant energy of a parcel and can provide a means of estimating the strength of any convection that may occur. CAPE can also provide an estimate of the maximum updraft intensity in a thunderstorm.
wmax is the estimated maximum vertical motion as a result of CAPE.
Convective Inhibition, or CIN is essentially negative CAPE, also in J·kg–1. It is the negative area between the parcel path and the environmental temperature curve where the parcel is cooler than the environment. The larger the value of CIN, the greater the negative buoyant energy that acts against CAPE. CIN sometimes acts as a "cap" on convection. If you have large CAPE but also large CIN, your CAPE may not be fully realized as buoyant energy and you may not have any convection. However, if your parcel is able to break through the cap, that is, if it is able to rise and become warmer than the environment, convection may be strong.
The figure below shows the locations of the LFC and EL, and shades in both positive and negative areas between the parcel path and the environmental temperature profile.

In the Lihue and Hilo soundings shown previously, values of CAPE and CIN are given in J·kg–1 in the column on the right hand side. Note that CIN is written as "CINS" and denoted as a negative value.
Locating the Tropopause
Recall that the standard temperature decreases with height within the troposphere, but becomes isothermal with height within the the tropopause, and increases with height in the stratosphere. With this knowledge, the location of the tropopause, given by its pressure level, can be determined by examining a plotted sounding. In the upper part of your sounding, look for where the temperature profile becomes isothermal (parallel to your skewed isotherms) or for an inversion (where the temperature increases with height, which will be tilted to the right more than your isotherms). The base of the isothermal layer in your sounding is the tropopause.

There are many things we can learn about the atmosphere from Skew-T Log-P diagrams. Here we've provided just the basics to get you started.
Chapter 5: Questions to Consider
- Drag and drop terms to their correct position in the atmospheric stability diagram below:
- What does the Lifting Condensation Level (LCL) represent? How can it be found on a Skew-T diagram?
- What is CAPE? How can it be found on a Skew-T diagram?
Selected Practice Question Answers:
Source: http://pressbooks-dev.oer.hawaii.edu/atmo/chapter/chapter-5-atmospheric-stability/
Postar um comentário for "Air That is Pushed Upward and Continues to Move Upward is Defined as"